どうもこんにちは。
コンです。
みなさんは、画像のエッジ検出を行なったことがありますでしょうか？？
Pythonを使っていても学校の授業でやったことある、だったりやったこと無い人もいるとは思います。
実はこのエッジ検出はとても便利で
画像処理では色々な所で使われます。
例えば下の例でいうと、背景と写っているものが同じグレーで2値が難しいようなケースでも
エッジ検出ともフォロジーを組みわせることで、2値化が可能になったりします。
今日はそんなエッジ検出の基本をPythonを使って実装していきます。
 | 【新品】コンピュータ画像処理 田村秀行/編著 斎藤英雄/編著 価格:4,290円 |
まえおき
基本のエッジ検出ということで最初は微分フィルタとソーベルフィルタから
Numpy、matplotlibライブラリを使って実装していきたいと思います。
今回も神奈川工科大学さんのwebサイトから標準画像データベースSIDBAを使わせてもらいました。
今回は縦と横の線がはっきりしているText.bmpを使ってエッジ検出をしていきます。
以前の記事では、フィルターというものを使って、特定の画素とその周辺の領域内の画素をまとめて計算するという空間フィルタリングというもの紹介させていただいておりました。
こちらの知識があると、より今回の記事が面白く感じるかもしれません。
微分フィルタ
微分という難しい言葉を使っておりますが、要するに
となり同士の画素の値の差分を計算する！！
というだけです。
このフィルタをかけると、隣同士の画素値に変化がないところは出力が0になるので
エッジが検出されるというわけです。
実例
下の図に微分フィルタの一例を示してみます。
①は中央の画素と右隣の画素との差を計算するフィルタで、②は中央と左隣の画素との差を計算するフィルタです。③は中央の両隣の差分の平均のフィルタになります。
①〜③は横方向について計算しておりますが、④〜⑥は縦方向を計算するフィルタになります。
実際に上の微分フィルタをText.bmpにかけた結果がこちらです。
この画像の上に書かれた①~⑥、は上の微分フィルタの①〜⑥に対応しております。
横方向の微分フィルタ①〜③によって画像の縦の線が明確になっていて
④〜⑥は逆に画像の横の線が明確になっていることがわかります。
①②と③、④⑤と⑥とで計算方法が少しだけ違うので、結果も少し違うようにみえますね。
実装コード
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import math
from PIL import Image
#横方向のフィルタ
def horizontal_filter(parameter):
if parameter == 'a':
filter = np.array([[0, 0, 0], [0, -1, 1], [0, 0, 0]])
elif parameter == 'b':
filter = np.array([[0, 0, 0], [-1, 1, 0], [0, 0, 0]])
else:
filter = np.array([[0, 0, 0], [-1/2, 0, 1/2], [0, 0, 0]])
return filter
#
def vertical_filter(parameter):
if parameter == 'a':
filter = np.array([[0, 1, 0], [0, -1, 0], [0, 0, 0]])
elif parameter == 'b':
filter = np.array([[0, 0, 0], [0, 1, 0], [0, -1, 0]])
else:
filter = np.array([[0, 1/2, 0], [0, 0, 0], [0, -1/2, 0]])
return filter
#畳み込み
def convolve2d(image, filter):
shape = (image.shape[0] - filter.shape[0] + 1, image.shape[0] - filter.shape[0] + 1) + filter.shape
strides = image.strides * 2
strided_image = np.lib.stride_tricks.as_strided(image, shape, strides)
return np.einsum('kl,ijkl->ij', filter, strided_image)
im = np.array(Image.open('Text.bmp'))
print('画像の大きさ', im.shape)
parameter_list = ['a', 'b', 'c']
#描画
fig, axes = plt.subplots(2, 3)
for i in range(2):
for j in range(3):
if i == 0:
output = convolve2d(im, horizontal_filter(parameter_list[j]))
else:
output = convolve2d(im, vertical_filter(parameter_list[j]))
axes[i][j].axis("off")
axes[i][j].imshow(output, cmap = "gray")
#描画
plt.show()
plt.close()今回はmatplotlibのsubplotをfor文で書いてみました。
for文の書き方はこちらのブログを参考にさせていただきました。
ソーベルフィルタ
微分フィルタの弱点としては 「ノイズを強調してしまう」という点があります。
これはどうしてかというと、隣同士の変化を強調してしまうので
画素値が急激に変化するノイズは微分フィルタによってその差が顕著に出力されます。
そこで微分フィルタをかけたあとに、かけた微分フィルタと逆方向に平滑化フィルタをかけることで
微分フィルタをかけたことによるエッジを残しつつ、ノイズを低減するという手法もあります。
実例
今回はソーベルフィルタを実装していきます。
フィルタは下のような感じになります。
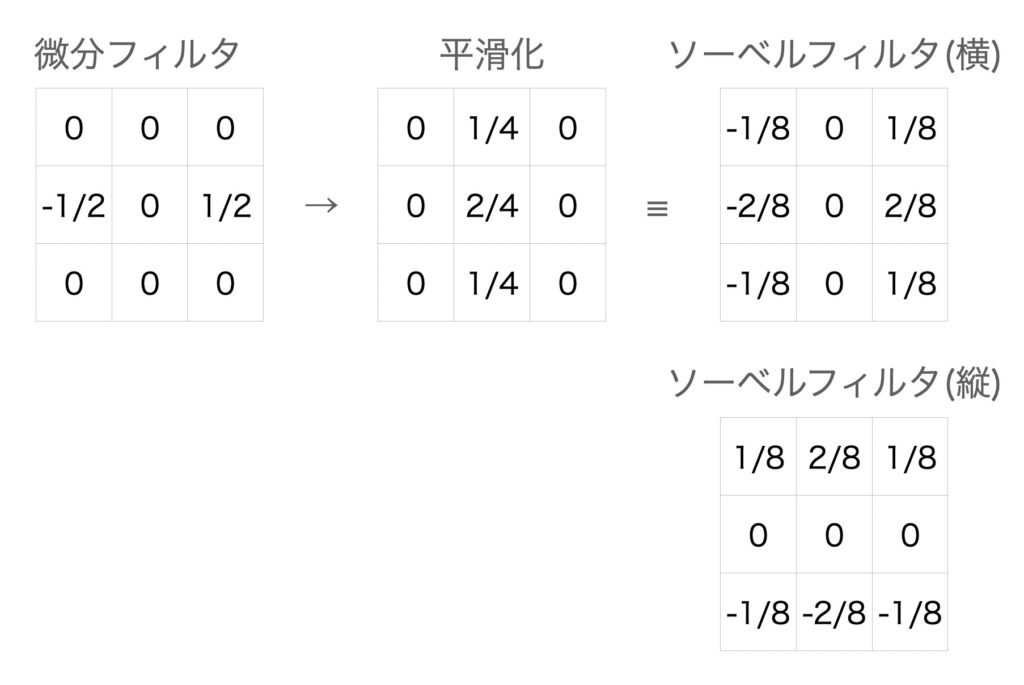
ソーベルフィルタは中央に重みをかけてます。
これをText.bmpにかけてみた結果が以下のようになります。
左が微分フィルタ(③と⑥)で、右がソーベルフィルタです。
これ違いが分かりましたか？？
私は分かりませんでした(笑)
なので部分的に拡大してみました。
これを確認すると、確かに平滑化がされており、
特に右下の横線のエッジに関しては、微分フィルタりもくっきりとした線になったかと思います。
実装コード
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import math
from PIL import Image
#横方向のフィルタ
def horizontal_filter(parameter):
if parameter == "derivative" :
filter = np.array([[0, 0, 0], [-1/2, 0, 1/2], [0, 0, 0]])
else:
filter = np.array([[(-1/8), 0, (1/8)], [(-2/8), 0, (2/8)], [(-1/8), 0, (1/8)]])
return filter
#縦方向
def vertical_filter(parameter):
if parameter =='derivative':
filter = np.array([[0, 1/2, 0], [0, 0, 0], [0, -1/2, 0]])
else:
filter = np.array([[(1/8), (2/8), (1/8)], [0, 0, 0], [(-1/8), (-2/8), (-1/8)]])
return filter
#畳み込み
def convolve2d(image, filter):
shape = (image.shape[0] - filter.shape[0] + 1, image.shape
- filter.shape + 1) + filter.shape
strides = image.strides * 2
strided_image = np.lib.stride_tricks.as_strided(image, shape, strides)
return np.einsum('kl,ijkl->ij', filter, strided_image)
im = np.array(Image.open('Text.bmp'))
print('画像の大きさ', im.shape)
parameter_list = ['derivative', 'sobel']
#描画
fig, axes = plt.subplots(2, 2)
for i in range(2):
for j in range(2):
if i == 0:
output = convolve2d(im, horizontal_filter(parameter_list[j]))
print(parameter_list[j])
else:
output = convolve2d(im, vertical_filter(parameter_list[j]))
print(parameter_list[j])
axes[i][j].axis("off")
axes[i][j].imshow(output, cmap = "gray")
#描画
plt.show()
plt.close()上のコードとあんまり変わらないです。
本当はfor文のところを、もうちょっとかっこよく書いてみたかったんですが
諦めてしまいました。。。
おわりに
ここまで読んでいただき、ありがとうございました！！
普段はYoloとかSSDだったりの物体検出の深層学習を使っているのですが
本当はプログラムの内部でエッジ検出をしているはずなのですが、自分があまり考えていなかったので
今回の記事を機に、勉強して書かせてもらいました。
また読んでいただければ幸いです。
